مثلثات شاخه گستردهای از علم ریاضی است که به بررسی روابط بین زاویههای اضلاع یک مثلث میپردازد. مبحث مثلثات در علوم دیگری همچون فیزیک، نقشهبرداری و نجوم نیز کاربرد دارد. به کمک مثلثات میتوانیم فاصلهها را به صورت غیرمستقیم اندازه بگیریم.
در روابط مثلثاتی به یک مثلث خاص نیاز داریم. به یک مثلث با زاویه راستگوشه، گونیا یا قائمه متمرکز میشویم. مشخص است که اگر یک زاویه یا گوشه از مثلثی قائمه باشد، به آن مثلث قائمالزاویه یا «مثلث راست گوشه» گفته میشود. این مثلث از آن جهت مهم است که قضیه فیثاغورس در مورد اضلاع آن صادق است.
تعریفی از نسبت های مثلثاتی از روی مثلث قائم الزاویه:
sin (سینوس): نسبت طول ضلع مقابل به طول وتر.
cos (کسینوس): نسبت طول ضلع مجاور به طول وتر.
tan (تانژانت): نسبت طول ضلع مقابل به طول ضلع مجاور.
cot (کتانژانت): نسبت طول ضلع مجاور به طول ضلع مقابل.
تابعهای مثلثاتی برای زاویههای تند بر اساس رابطههای بالا محاسبه میشوند. برای زاویههای بزرگتر از ۹۰ درجه، میتوان از مفهوم دایره مثلثاتی بهره گرفت.
دایره مثلثاتی
دایره ای است به شعاع یک واحد که خلاف جهت عقربه های ساعت را جهت مثبت در نظر می گیریم و مرکز آن مبدا مختصات است. محورهای مختصات دایره را به 4ناحیه (ربع) تقسیم میکنند. ربع بالا سمت راست ربع اول، ربع بالا سمت چپ ربع دوم، ربع پایین سمت چپ ربع سوم و ربع پایین سمت راست ربع چهارم نامیده می شود. با توجه به این که شعاع دایره به اندازه واحد است، مقدار نسبت های مثلثاتی زاویه ? را می توان روی دایره نشان داد.
| ربع اول | ربع دوم |
| ربع چهارم | ربع سوم |
اتحاد
اگردوعبارت جبری A و B به گونه ای باشند كه به ازای هرمقداری كه به متغيرهايشان داده ميشود، حاصل يكساني داشته باشند. در اين صورت تساوی A=B یک اتحاد ناميده مي شود.
اتحاد مثلثاتی
هر یک از روابطی که بدست آوریم و به ازای هر ? برقرار است را یک اتحاد مثلثاتی مینامیم. حال این سوال پیش میآید که یک عبارت را چه وقت یک اتحاد مثلثاتی مینامیم؟ هرگاه بتوانیم از یک طرف تساوی به کمک روابط مثلثاتی به طرف دیگر تساوی برسیم، یک تساوی(اتحاد) بین دو عبارت مثلثاتی برقرار خواهد بود.
در بین نسبت های مثلثاتی روابط زیبایی وجود دارد که میتوان با داشتن چند نسبت و رابطه ساده، بقیه نسبت ها را نیز بدست آورد. این روابط که همان اتحادهای مثلثاتی هستند کاربردهای زیادی در ساده کردن روابط و حل معادلات مثلثاتی دارند.
در زیر ده نمونه از این نسبت ها و اتحاد ها آورده شده است که به کمک آن ها میتوان برابری های زیادی را ساده و اثبات نمود.
اتحادهاي مثلثاتي مهم
| |
| |
| |
| |
| |
| |
| |
| |
همچنین
| |
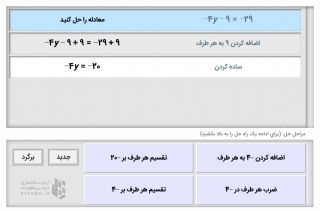
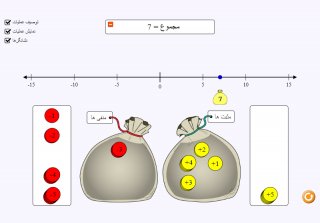
نحوه کار با شبیه ساز
اتحادی که نمایش داده شده را ساده کنید که این کار را به کمک یکی از چهار گزینه ای که در پایین صفحه قرار دارد انجام میدهید. گزینه مورد نظر را به روی صفحه بالا بکشید. اگر گزینه درست انتخاب شده باشد مرحله بعدی ساده سازی را انجام میدهید در غیر این صورت بدنبال پاسخ درست بین گزینه ها باشید. در هر مرحله از حل میتوانید با انتخاب گزینه "برگرد" به مرحله قبل بازگردید. بعد از اتمام ساده سازی در پایین صفحه برابری رابطه مثلثاتی انجام شده برای شما نمایش داده میشود. در نهایت برای انتخاب سوال جدید روی گزینه "جدید" کلیک کنید.
شما دانشآموز و دانشجوی عزیز با استفاده از مثالهایی که در این شبیه ساز مشاهده نمودید، میتوانید روابط بیشتری را با کمک اتحادها اثبات کنید. با انجام این تمرینات مجازی خواهید فهمید که این کار تا چه حد لذت بخش بوده و چقدر راحت میتوان یک اتحاد مثلثاتی را اثبات کرد. اینکار همچنین به فهم بیشتر شما از ریاضیات کمک خواهد کرد.
فعالیت
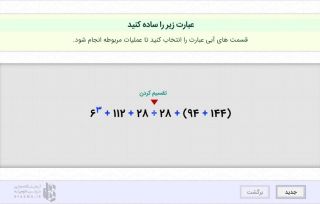
عبارت زیر را ساده کنید.
A) =
B) =
C) =
D) =
- مطالعه نسبت های مثلثاتی
- آشنایی با اثبات اتحادهای مثلثاتی
- توانایی حل و ساده سازی اتحادهای مثلثاتی